Fourth Grade. Slide 1 / 146. Slide 2 / 146. Slide 3 / 146. Multiplication and Division Relationship. Table of Contents. Multiplication Review
|
|
|
- Andrea Harvey
- 5 years ago
- Views:
Transcription
1 Slide 1 / 146 Slide 2 / 146 Fourth Grade Multiplication and Division Relationship Table of Contents Slide 3 / 146 Click on a topic to go to that section. Multiplication Review Properties of Multiplication Factors Prime and Composite Numbers Multiples Inverse Operations
2 Links to PARCC sample questions Slide 4 / 146 End of Year Non-Calculator #23 Non-Calculator #28 Non-Calculator #32 Slide 5 / 146 Multiplication Review Return to Table of Contents Multiplication is a fast way of adding a series of repeated numbers Using repeated addition or skip counting: Slide 6 / X 3 means X 3 = 15 4 X 8 means X 8 = 32 Or you can use a picture model: 5 x 2 = 10 s Write an example of a multiplication sentence related to addition and solve it.
3 Place Value and Multiplying Remember how each place value is 10 x's larger than the next? Slide 7 / 146 If we take any of the place value units, the next unit on the left is ten times as many. 1 ten = 10 x 1 one (1 ten is 10 times as much as 1 one) 1 hundred = 10 x 1 ten 1 thousand = 10 x 1 hundred Place Value and Multiplying Slide 8 / 146 We can apply this knowledge with larger numbers whose digits are in the tens, hundreds, or even thousands! 10 x 3 = x 3 = 300 1,000 x 3 = 3,000 We know these are true because our place value is increasing by 10x's with each equation. Place Value and Multiplying We know that if a number is increasing in place value, we need to add the additional place value to our answer. Slide 9 / 146 Let's look at some examples: 4 x 4 = 16 4 x 40 = x 40 = 1,600 5 x 4 = x 4 = x 40 = 2,000 Can you see how the place value is getting larger with each equation? Do you notice a pattern? It is important to understand how place value works, but there is a TRICK when multiplying numbers that end in zeros!
4 What is the Trick? Slide 10 / 146 What is 6 x 7 =? What if we multiplied 60 x 7 =? First, we know the place value increases. You can also use the zero trick by covering up the zero, multiplying 6 x 7, which equals 42, then add the zero back onto your answer. 60 x 7 = 42 Add zero to end to show 60 x 7 = 420 What is 50 x 2 then? What about 70 x 80 =? Be careful, in this problem you have to cover 2 zeros, which means you have to add 2 zeros at the end! Use the Trick Slide 11 / 146 What is 50 x 2 then? What about 70 x 80 =? (Be careful, in this problem you have to cover up 2 zeros, which means you have to add 2 zeros at the end!) Use the Trick Slide 12 / 146 Try these: 400 x 3 = 20 x 50 = 8 x 900 = 10 x 100 = 70 x 40 = 300 x 90 =
5 1 What would the multiplication number sentence look like for the repeated addition problem, ? Slide 13 / 146 A B 7 x 7 C 7 x 4 D 4 x 4 Slide 14 / What would the addition sentence look like for 3 X 4? A B C D What is the answer to 90 x 80 =? Slide 15 / 146 A 72 B 720 C 7,200 D 72,000
6 4 Select the statement that explains how the numbers 55 and 550 are different. Slide 16 / 146 A 550 is 1000 times larger than 55. B 550 is 100 times larger than 55. C 550 is 10 times larger than 55. D 550 is 1 times larger than What is 40 x 600 =? Slide 17 / 146 A 2,400 B 24,000 C 240 D 24 The numbers in a multiplication sentence are represented by factors and the product. - Factors - numbers you multiply together to get another number - Product - the answer when 2 or more numbers are multiplied together Slide 18 / 146 Here are 2 ways to write a multiplication sentence. 2 X 5 = 10 factor product factor 2(5) = 10 factor factor product
7 6 Using the multiplication sentence, 6 x 8 = 48 Which number is the product? Slide 19 / Using the multiplication number sentence, 9 x 5 = 45 Which numbers are factors? Slide 20 / 146 A 9 B 5 C 45 D 0 8 What is the product for 6 x 6? Slide 21 / 146
8 9 What is the product for 7(9)? Slide 22 / 146 Arrays Multiplication sentences can also be represented using picture models called arrays. Slide 23 / 146 For example: 2 X 5 means X 5 = 10 4 X 6 means X 6 = means 3 X 4 3 X 4 = 12 Arrays Array sentences are written with the number of rows first and the number of columns second. Slide 24 / 146 columns rows columns rows 4 x 2 2 x 4 Create a multiplication sentence, draw a picture to represent your values.
9 Arrays Slide 25 / 146 Drag arrows into each rectangle to make the arrays. How are they the same? Different? 5 x 2 2 x 5 Arrays 1.On a dot paper, draw several arrays 2.Trade your paper with a partner and label your partners arrays with the appropriate multiplication sentence inside or next to the drawing. Slide 26 / 146 Example: 8 X 3 = 24 Slide 27 / 146
10 10 Which array is a model for 3 x 4? Slide 28 / 146 A C B D none of the above 11 This array shows: Slide 29 / 146 A 1 x 3 B 3 x 1 C 3 x 0 D 0 x 3 12 Which array is circled? Slide 30 / 146 A 5 x 8 B 2 x 4 x 5 C 8 x 5 D 10 x 7
11 Slide 31 / 146 Properties of Multiplication Return to Table of Contents Multiplication Properties They make solving multiplication easier! Slide 32 / Zero Property 2. Identity Property 3. Commutative Property 4. Associative Property 5. Distributive Property 3 X 0 = 0 4 X 1 = 4 5 X 6 = 6 X 5 2 X (3 X 4) = (2 X 3) X 4 9(20-3) = (9 X 20) - (9 X 3) These properties are directly related to the addition properties you learned previously! Multiplication Properties Discuss with an elbow partner, what do all of these equations have in common? Slide 33 / X 0 = 0 m X 0 = 0 0 X 32 = 0 0 X R = 0 0 X 564 = 0 7,895 X 0 = 0 Based on these examples, what do you think 5,280 X 0 =?
12 Zero Property Slide 34 / 146 Any number multiplied by 0 is always zero 0 X 3 = = 0 6 X 0 = 0 You can also use variables to represent any value 0 X m = 0 Try this: If Jackie has 5 hats and zero marbles in each hat. How many marbles does she have in all? Identity Property Slide 35 / 146 Any number multiplied by ONE is always the original number 5 x 1 = 5 1 X 2,345,407 = 2,345,407 Try this: Solve for p in the following: 234 X p = 234 What tools did you use to find your answer? Tell a partner. Multiplication Properties Slide 36 / 146 Solve the following equations. Write what multiplication property is represented in all 3 equations, then discuss how you determined the value of the variable in each one. Property: X 1 = z 2.q X 2,567 = 2, ,765 X d = 98,765
13 13 Is 7 X 0 = 0 an example of the Zero Property? Slide 37 / 146 Yes No 14 Which equation is representing the Identity Property? Slide 38 / 146 A 8 X 8 = 64 B 90 X 1 = 1 C 36 X 2 = 36 X 2 D 4 X 1 = 4 Commutative Property Slide 39 / 146 The commutative property of multiplication means the order of the numbers does not change the result (answer) of the problem 3 X 5 is the same as 5 X 3 (They both equal 15) To remember this property, think of communicating (talking) with your friends! Here are some more examples: a x b = b x a 3 x 8 = 8 x 3 Try This: How can you finish the equation using the Commutative Property? 7 X 4 =? X?
14 Associative Property Slide 40 / X (2 X 4) = (3 X 2) X 4 (8 X 3) X 9 = 8 X (3 X 9) 4 X (7 X 6) = (4 X 7) X 6 Talk it out: Looking at the examples to the left, how would you define the Associative Property in your own words? Click inside the box for definition. Associative Property Slide 41 / 146 Is this Associative? 6 X (5 X 2) = (2 X 5) X 6 Watch out! No, because the order of the numbers changed, Click here for the answer... not the parenthesis. Commutative and Associative Properties Move the definitions and examples below to the appropriate column. Slide 42 / 146 Commutative Associative Keeps the same numerical order, but parenthesis move 3 X 5 = 5 X 3 Can reorder numbers in the expression 5 X (7 X 2) = (5 X 7) X 2
15 Distributive Property Slide 43 / 146 In the Distributive Property, you distribute, pass, or hand out multiplication to numbers within parenethsis using addition or subtraction. There are 2 common ways to use this property Distributive Property Slide 44 / 146 #1: You can use it to find math facts that can be difficult to remember... Lets solve 6 X 12 = A by distributing 6 into parts of 12 Step 1: Break 12 into easier numbers you can multiply. We know = 12, right? So... Step 2:...if we distribute (pass out) 6 to both digits, we will have (6 X 10) + (6 X 2) Step 3: Solve the equation starting with multiplication. 6 X 10 = X 2 = = 68 What is another way you could distribute 12 to solve? Let's Practice! Slide 45 / 146 How can you solve 8 x 13 by using the Distributive Property? First, let's think of an easy way to break apart the larger number... What are possible numbers that add up to equal 13? Does it make more sense to use = 13 or = 13? Why? Let's use , so applying the Distributive Property to solve would look like this... 8 x 13 = (8 x 10) + (8 x 3) = = 104 Derived from
16 Let's Practice! Slide 46 / 146 How can you solve 8 x 13 by using the Distributive Property? Can you solve 8 x 13, by distributing 13 using the numbers 8 and 5? What is your answer? Derived from Your Turn Slide 47 / 146 With your elbow partners solve the following using the distributive property. Remember to first decide what 2 numbers make the larger number easier to solve with. For example, in #1, does it make more sense to break 12 into or ? Show your work! 6 x 12 = 34 x 8 = 42 x 4 = Distributive Property #2 You can solve an equation with parenthesis by distributing the number on the outside to digits on the inside. Slide 48 / 146 Remember a number next to parenthesis means to multiply! 6(9 + 5) = (6 X 9) + (6 X 5) = 75 You use addition after you find the products because that is the function inside the parenthesis. Try this using the distributive property: 9(8 + 6) =
17 Distributive Property Slide 49 / 146 You can also use it with subtraction. Instead of adding the products together, you will subtract them. Notice subtraction being carried throughout since it is function within the parenthesis 8(7-3) = (8 X 7) - (8 X 3) = 32 Try this using the distributive property: 3(6-4) = Let's Practice! Slide 50 / 146 Click on the picture below to check your understanding of multiplication properties. You can take turns shooting hoops and answering questions! 15 Which number sentence demonstrates the Distributive Property? Slide 51 / 146 A 6(4 X 2) = 6(2 X 4) B 3 X (2 X 1) = (3 X 2) X 1 C 5 x 32 = (5 X 30) + (5 X 2) D None of them
18 16 A candy company has orders for chocolate bars from 5 different stores. Each order contains 45 chocolate bars. Choose the equation you should use to figure out how many chocolate bars the candy company needs to make. Solve. Slide 52 / 146 A 4 x 50 = chocolate bars B (45 x 5) - (45 x 5) = chocolate bars C (30 x 5) + (5 x 5 ) = chocolate bars D (5 x 40) + ( 5 x 5) = chocolate bars 17 Is 8 X (9 X 3) = 9 X (8 X 3) an example of the Associative Property? Explain your answer. Slide 53 / 146 True False 18 Which set of equations show the Associative Property? *remember the numbers are socializing! Slide 54 / 146 A 9 X 5 X 4 = 5 X 4 X 9 B 3 X (54 X 6) = (3 X 54) X 6 C 2 X 0 = 0 D 2(5-4) = (2 X 5) - (2 X 4) Answer
19 19 In the Commutative Property, you can switch the numbers around and still get the same answer. Slide 55 / 146 Yes No 20 Which two equations represent the statement "48 is 6 times as many as 8?" Select the two correct answers. Slide 56 / 146 A 48 = B 48 = 6 x 8 C 48 = 6 x 6 D 48 = E 48 = 8 x 6 From PARCC sample test 21 Rewrite the expression 8(4 + 3) using the Distributive Property of Multiplication. Then simplify your answer. Slide 57 / 146
20 22 What property is being represented by 8 X 3 = 24; 3 X 8 = 24? Slide 58 / 146 A Identity Property B Commutative Property C Associative Property D Zero Property Answer Slide 59 / Which property is being demonstrated in 7 x 16 = (7 X 10) + (7 x 6) A Distributive Property B Associative Property C Idenity Property D Commutative Property 24 Which property is shown? 5 x 4 = 20 4 x 5 = 20 Slide 60 / 146 A B C D Identity Commutative Zero Same Answer
21 25 Which set of number sentences show the commutative property? Slide 61 / 146 A 7 x 3 = = 21 B 4 x 1 = 4 0 x 4 = 0 C 8 x 2 = 16 2 x 8 = 16 D = = 6 Slide 62 / 146 Factors Return to Table of Contents What is a Factor? Slide 63 / 146 What is the multiplication sentences represented by these arrays? click to reveal 1 X 8 = 8 2 X 4 = 8 Both arrays equal the product of 8. Remember, factors are 2 numbers multiplied to get a given product. Factors, 1 X 8, and 2 X 4 both multiply to equal the product 8. So we know the factors of 8 are: 1, 2, 4, 8 Derived from
22 What is a Factor? Slide 64 / X 8 = 8 2 X 4 = 8 You can represent given factors by using a factor rainbow. Derived from Factor Rainbows Factor Rainbows help organize the numbers and allow you to check your work to make sure you find ALL factors. Slide 65 / 146 Lets factor 12: Look at the following arrays. What multiplication sentence are they showing? 1 X 12 =12 2 X 6 =12 Circle the factors. Write these factors in numerical order using the factor rainbow. Derived from Factor Rainbows Slide 66 / 146 Draw another array to represent another pair of factors for 12. Now rewrite all the factors found for 12 using a factor rainbow. click to reveal 3 X 4 = Derived from
23 Helpful Hints 1.Always start factoring with the number and 1. 2.Even numbers always have 2 as a factor. You will need to find the number that multiplies with 2 that equals the given number to know the factor pair! 3.Numbers with 5 as a factor have a 0 or 5 in the ones place value. 4.If you make a factor rainbow, and cannot connect a number to another factor it could be... - You forgot to find the other factor and should do so. - The other factor is the same number. Slide 67 / 146 Helpful Hints Slide 68 / 146 For example: Take the number 9. The factors are 1, 3, 9 Discuss with your partner why 3 does not have a factor pair, but this factor rainbow is correct. click to reveal The number 3, does not have a factor to connect to because 3 x 3 = 9. This number only needs to be written once! 26 Is there a factor missing from this factor rainbow for the number 16? Slide 69 / 146 Yes No
24 How do you know you've found ALL the factors? Lets factor 18: 1. We always start with 1 and the number, in this case Then you continue to think of numbers and/or draw arrays that multiply to represent 18. Work up numerically, going to 2, then 3, and so on. If it doesn't multiply by another factor to equal 18, you know it's not a factor. 3. You will be able to make the factor rainbow, connecting each factor pair when you have found all of the factors! Slide 70 / 146 Think through it! Factor pairs of Check your factor pairs, make sure you didn't forget one or more! Partner Up and Try This Factor the following numbers using the strategies you've just learned. 30: 1, click 2, 3, 5, 6, 10, 15, 30 Slide 71 / : 1, click 2, 3, 4, 6, 8, 12, 24 45: 1, 3, 5, 9, 15, 45 click How can we check our work to make sure we have all the factors?...by using a factor rainbow click Lets check our work! Division with Factors Division can help to find factors of larger numbers Slide 72 / 146 Lets look at the number 54. How can we determine if 3 is a factor of 54? Use division to determine if 3 is a factor or not: 54 3 =? Because there is no remainder, you know that 3 is a factor of and 18 are a factor pair of 54 Use division when unsure of numbers that could be factors!
25 Division with Factors How can you find all the factors of 54? Slide 73 / 146 Let's find out together... 1.Begin with 1 and the given number, 54 2.Because 54 is even, we know 2 is a factor and 27 are factors Could you skip count to 1 4 find the missing factor as well? Previously we found 3 and 18 are factors. 4. Then 4 and so on, until you each 12. Is it necessary to divide to find if 5 is a factor of 54? Factors Using the strategies we just covered, multiplication facts and division, let's find the factor pairs of 60. Factor 60: 1. We know 1 and 60 are the beginning factors 2. Now we think about the number 2, is 60 an even or add number? It's even so 2 is a factor - now we need to find how many 2s 3. What about 3? Let's use division to find out Now we need to look at 4. Use division again. Factor Pairs Now keep working through the digits until you find the rest of the factors. What are all of the factors? Slide 74 / 146 Analyzing the Numbers Is 6 a factor of 54? If we know 6 is a factor can we say that 2 and 3 are also factors of 54? Is the following multiplication sentence true? 54 = 6 x 9 = (2 x 3) x 9 Slide 75 / 146 If we rewrite it vertically we can see how 6 relates to 2 and 3 54 = 6 x 9 = (2 x 3) x 9 Remember the Associative Property? Lets use it to socialize 3 with 9 to check if 2 and 3 are really factors. 54 = 2 x (3 x 9) 54 = 2 x = 54 This proves 2 and 27 are a factor pair of 54 Derived from Associative Property can help us find factors!!!
26 Let's Practice using Associative Property Slide 76 / 146 Is 6 a factor of 42? How do you know... We know 6 is factor because click 6 x 7 = 42 Let's use the Associative Property to determine if 2 and 3 are also factors of = 6 x 7 42 = (2 x 3) x 7 42 = 2 (3 x 7) 42 = 2 x = 42 Associative property at work! We can see that 2 is a factor of 42 because 2 and 21 are a factor pair that multply to equal 42! Derived from Factors Slide 77 / 146 Get with an elbow partner and answer the following. What is 6 x 12? Work with your partner to prove 6 is a factor of 72, so 2 and 3 must also be factors using the associative property.. Now find all of the factors of 72. Show your work. 27 Is 5 a factor of 75? Show how you know on paper and be prepared to explain your answer. Slide 78 / 146 Yes No
27 28 Select all of the factors for the number 27. hint: Make sure you think through each possible factor and make a factor rainbow before choosing an answer! Slide 79 / 146 A 1 B 2 C 3 D 4 E 5 F 8 G 9 H 12 I 14 J If 8 is a factor of 56, can we also say that 4 and 2 are factors? Show your work and be ready to explain. Slide 80 / 146 Yes No 30 Select the three choices that are factor pairs for the number 28. Slide 81 / 146 A 1 and 28 B 2 and 14 C 3 and 9 D 4 and 7 E 6 and 5 F 8 and 3 From PARCC sample test
28 31 Which correctly lists all of the factors for 40? Slide 82 / 146 A 1, 40 B 1, 2, 3, 4, 5, 8, 9, 10, 20, 40 C 1, 2, 4, 5, 8, 10, 20, 40 D 1, 2, 20, Which correctly lists all of the factors for 31? Slide 83 / 146 A 1, 31 B 1, 3, 31 C 1, 3, 9, 31 D 1, 3, 7, 9, Which number is a factor of 22? Slide 84 / 146 A 44 B 6 C 8 D 2
29 34 Which number is a factor for 63? Slide 85 / 146 A 6 B 10 C 3 D 2 35 What factors can you use in the following equation to make a product that is an odd number between 30 and 60? Mark the answer with all possible solutions. X 5 = Slide 86 / 146 A 6, 7 and 8 B 7, 9 and 11 C 7, 9, 11 and 13 D 6, 7, 8, 9, 10 and 11 Using Factors with Area Imagine Suzie and her friend trying to build a sand castle. They want the castle to be 24 square feet when they are done. What are possible side lengths their castle could have? Slide 87 / 146 Using our knowledge of factors and area, we can create different lengths of the sides. Remember the area formula is length x width A = L x W 2 2 x 12 = We know 2 and 12 are a factor pair of 24 so we can make a castle area using these as dimensions. 3 3 x 8 =24 8 Suzie could also build her castle 3 by 8 feet.
30 Using Factors with Area Slide 88 / 146 Dillion needed to build a parking lot for the new high school. They needed it to be 100 square yards total in size. What are 3 possible dimensions Dillion could use to make his parking lot? 36 Craig's family decided that wanted to build a local neighborhood park. The city gave them 45 square yards to design their park in. What are possible dimensions that could have used to create it? (Select all that apply.) Slide 89 / 146 A 1 yard by 45 yards B 2 yards by 25 yards C 4 yards by 9 yards D 5 yards by 9 yards E 7 yards by 7 yards Slide 90 / 146 Prime and Composite Return to Table of Contents
31 Determining Prime/Composite Numbers Slide 91 / 146 Let's Think: When determining if a number is Prime or Composite, you have to think about the factors. What do you currently know about factors? How do you solve for factors? What do you use to check your work? Prime Numbers Let's look: 1 X 7 = 7 What are the factors of this equation? 1 and 7 are the only factors. click How do you know? Slide 92 / 146 Think about 1 X 5 = 5 What are the factors of this equation? 1 and 5 are the only factors. click Derived from Prime Numbers Slide 93 / 146 Numbers like 5 and 7 that only have 2 factors, 1 and itself, are called prime numbers.
32 Prime Numbers Practice Slide 94 / 146 Try this: Create a list of at least 2 other prime numbers with a partner. Remember, a prime number only has 1 and itself as factors. Composite Numbers Numbers with multiple factors are called composite numbers. Slide 95 / 146 Lets look at the number 8: Factors Pairs of We can see 8 is a composite number because it has more than 1 and itself as factors. There are 4 factors of 8. The factor pair 2 and 4 make it a composite number. Composite Numbers Slide 96 / 146 Try this: Is the number 45 a prime or composite number? Work with a partner creating a visual representation of why or why not. (Remember we have used arrays, factor tees, or factor rainbows to show our work.)
33 Prime Sort the Numbers Composite Slide 97 / 146 Slide 98 / 146 In the case of 24, you can find the prime factorization by taking and dividing it by the smallest prime number that goes into 24: 24 2 = 12. Now divide out the smallest number that goes 12: 12 2 = 6. Now divide out the smallest number that goes in 6: 6 2 = 3. Since 3 is prime, you're done factoring, and the p factorization is 2 x 2 x 2 x 3. Exceptions Slide 99 / 146 There are 2 numbers that do not qualify as prime or composite. 0 and 1 0 is not classified by these terms because no matter what number you multiply it by, it is always zero. Therefore, 0 is neither prime or composite. 1 is not classified by these terms because mathematicians have agreed it is easier to define the structure of our number system without it classified. Therefore, 1 is neither prime nor composite. Derived from
34 Click for Game Slide 100 / 146 Slide 101 / Sasha says that every number in the twenties is a composite number because 2 is even. Amanda says there are two prime numbers in the twenties. Who is correct? How do you know? A Sasha Answer B Amanda 38 Which of the following numbers are prime? (Select more than one answer.) Slide 102 / 146 A 1 B 2 C 3 D 4 E 5 F 6
35 39 Which of the following numbers are composite? (Select more than one answer.) Slide 103 / 146 A 9 B 10 C 11 D 12 E 13 F Which of the following sets of numbers has all prime numbers? Slide 104 / 146 A 1, 2, 3, 5, 7 B 2, 3, 5, 7, 9 C 0, 1, 2, 3, 5 D 2, 3, 5, 7, If you complete the following equation. Is the answer a prime or composite number? Slide 105 / A Prime B Composite Answer
36 Slide 106 / Teacher Notes Circle the prime numbers to help the space shuttle to take off from Earth Slide 107 / 146 Multiples Return to Table of Contents What is a Multiple? Turn to a partner and skip count by 4s until your teacher says to stop! Ready? GO! Slide 108 / 146 Talk it out: What number did you land on? What are some things you noticed about the numbers while you were counting? Continue to skip count with your partner, starting where you left off until your teacher tells you to stop again. See if you notice any patterns this time. Derived from Talk it out: What did you notice this time?
37 What is a Multiple? When you skip count by any number, the numbers you say are called multiples. Slide 109 / 146 Let's keep talking: (small group or partners) Talk it out: How is a multiple different than a factor? How do we know that 20 is a multiple of 4? Is 20 a multiple of 5? How do you know? What about 6? Is 20 a multiple of 6? How do you know? Derived from What are multiples of 8? Multiples Slide 110 / 146 click 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, etc. Challenge question: We know that 2 X 4 = 8, right? We can reason that 8 is a multiple of 2 and 4 because if we skip count by 2, we get to 8, or if we skip count by 4, we also get to 8. If 8 is a multiple of 2 and 4, are multiples of 8 also multiples of 2 and 4? Let's find out by looking at 40, a multiple of 8: 40 = (5 X 4) X 2 40 = 20 X 2 Yes, 40 is a multiple of 2. Counting 2 twenty times, gets 40. Derived from 40 = 5 X 8 40 = 5 X (4 X 2) 40 = (5 X 2) X 4 40 = 10 X 4 Yes, 40 is a multiple of 4. Counting 4 ten times, gets 40. Finding Multiples between Slide 111 / 146 Take the number 84. Is 84 a multiple of the number 4? Think about ways you could solve this problem. When determining if a number is a multiple of another number you use skip counting, or you can also use division. This is very helpful with larger numbers is a multiple of 4 because when you divide it out, there are no remainders. factor 4 X 21 = 81 factor multiple
38 Slide 112 / 146 Click for interactive game practice. Slide 113 / List 3 multiples of 4. Slide 114 / 146
39 43 Select all of the multiples of 6. Slide 115 / 146 A 54 B 15 C 42 D 1 E 35 F 56 Answer 44 If you are trying to find multiples of 6, are you also finding multiples of 2 and 3? Slide 116 / 146 True False 45 If you know that 60 is a multiple of 6 ten times, is 60 also a multiple of 2? Slide 117 / 146 Yes No
40 46 How many times do you count 2 in order to reach 60? Slide 118 / 146 A 15 B 20 C 25 D Select each number that is a multiple of 8. Slide 119 / 146 A 1 B 2 C 4 D 8 E 20 F 24 G 36 H 58 I 64 J 80 From PARCC sample test 48 Select all of the multiples of 4. Slide 120 / 146 A 4 B 32 C 25 D 36 E 22 F 28
41 49 Megan s father won first place in a bicycle race. The race was divided into equal sections, each measuring exactly 7 miles in length. Which number could be the total number of miles of the race? Use your knowledge of multiples to solve. Slide 121 / 146 A 28 B 45 C 62 D 15 Hundreds Chart Activity Slide 122 / 146 By crossing out multiples of numbers, all of the prime numbers will be identified. Use red to cross out all the even numbers (2, 4, 6, etc.) Use green to cross out all the multiples of 3 (3, 6, 9, etc.) that remain. Use purple to cross out the multiples of 5 that remain. Use yellow to cross out the multiples of 7 that remain. Make a list of the remaining numbers. What kind of numbers are they? Slide 123 / 146
42 Slide 124 / 146 Click for answer Slide 125 / 146 Inverse Operations Return to Table of Contents Connecting our Learning Get with a partner and discuss: Slide 126 / 146 What are 2 math functions you have been repeatedly working with throughout this unit? click Multiplication and division Think about it 4 X K = 12 8 X 2 = Q B X 5 = 40 How do those functions work together when finding factors, multiples, and solving equations? How do you know the answer to each equation? What math function do you use to solve them?
43 Connecting our Learning When solving a given equation or expression, you can use inverse operations, to find the solution. Inverse operations are the opposite operations that undo each other. Slide 127 / 146 Now look at the examples from the previous page. Would you change your answer on what operation you use to solve it? What is different about how you solve the first example to the second one? 4 X K = 12 8 X 2 = Q B X 5 = 40 Multiplication and division are inverse operations. You can use each of them to undo the other in order to solve various equations. Click below to watch a video Slide 128 / 146 Slide 129 / 146 Helpful Hints with Inverse Operations Inverse operations are used to solve unknowns in an equation. An unknown can be represented using a,?, or a letter to stand for the missing number. A letter that stands for a missing number in an equation is called a variable. Multiplication and division are inverse operations. Addition and subtraction are inverse operations.
44 Inverse Operations Take the algebraic expression: 2m = 14 (Remember 2m means to multiply, 2 times the amount of "m".) Slide 130 / 146 Let's rewrite it so we see the multiplication sign: 2 x m = 14 Now, we need to "move" the 2 to the right side of the equation by dividing, which is the inverse operation of multiplication. 2 x m = m = 14 2 The last step is to solve. m = 7, because 14 divided by 2 equals 7. Fact Families Use Inverse Operations Fact Families are an easy way to use inverse operations. Take the numbers, 4, 7, and 28. These numbers create a fact family using multiplication and division. Slide 131 / x 4 = 28 4 X 7 = = = 7 is the division that undoes the multiplication of 7 x 4 Try this: 72 8 = 9 What inverse operation can you use to undo this equation? Write the new equation. Is there more than one way to write it? Inverse Operations Move equations to match each with its inverse. Slide 132 / = = = 6 6 x 10 = = 8 7 x 5 = 35 4 x 6 = 24 8 x 3 = 24
45 Working Out Word Problems Using inverse operations to help solve word problems is an important tool to learn. KAYLEE the Key will help guide you through the steps of problem solving. The K.E.Y.S. to Problem Solving K: Know the important information in the problem. Read the problem (more than once) and first find the main idea. (Main Idea = What is the problem asking you to find?) Find all the important information that supports the main idea. K E Y S E: Equation (or equations) is created to plan your strategy and organize the important information. Strategy must be organized and easy to follow. Use equations to develop a strategy (i.e. algorithm, diagram). Y: Yes, I have checked over my strategy and my answer is reasonable (makes sense). Use an estimate to check if your answer is reasonable. S: Solution is written with the correct label and explanation if needed Slide 133 / 146 Inverse Operations Word Problems Slide 134 / 146 The animal shelter has 18 kittens. The same number of kittens were born to each of 3 mother cats. How many kittens did each mother cat have? Pull out the information you need to solve. Write the equation to solve the unknown value: Solve 3 x = 18 3, K, 18 kittens 3 x = = 6 Write your answer: Each mother cat had 6 kittens. Inverse Operations Word Problems Slide 135 / 146 The cost of buying a movie is 4 times as much as renting one. It costs $20 to buy a movie. What is the cost, in dollars, of renting a movie? Pull out the information you need to solve. 4, R, and $20 Write the equation to solve the unknown value: 4 x r = $20 Solve 4 x r = 20 r = 20 4 r = $5 Write your answer: It costs $5 to rent a movie.
46 Inverse Operations Word Problems Slide 136 / 146 Try this: With a partner read the following, write an equation, and solve using inverse operations. A new video game you want is $42. How much money do you need to save per week if you want to buy it in 7 weeks. Inverse Operations Word Problems Slide 137 / 146 Try this: With a partner read the following, write an equation, and solve using inverse operations. Stan was playing a game with this friend. His friend was trying to guess the number he was thinking of. Stan told him if he multiplied his number by 2 and added 9 the answer would be 21. Write an equation. Then use inverse operations to solve. 50 Division and multiplication are inverse operations. Slide 138 / 146 True False
47 51 Which equation shows the inverse operation for the equation 63 9 = 7? Slide 139 / 146 A 3 x 7 = 63 B 7 x 9 = 63 C 21 3 = 7 D 63-9 = 54 Answer 52 Which equation shows the inverse operation for the equation 5 x 4 = 20? Slide 140 / 146 A 20 4 = 5 B 20 1 = 20 C 20 2 = 10 D 10 x 2 = Use inverse operations to solve for the unknown in the equation. Slide 141 / 146 y x 6 = 54
48 54 Use inverse operations to solve for the unknown in the equation. Slide 142 / ? = 9 55 Use inverse operations to solve for the unknown in the equation. Slide 143 / 146 x 8 = Sammy's friend was trying to guess what number he was thinking of. Sammy told him if you multiply by 2 the answer is 24. What is Sammy's number? Write the equation showing the unknown value and solve using inverse operations. Slide 144 / 146 A 10 B 48 C 24 D 12
49 57 Your teacher thinks of a number, divides it by 5 and then adds 19. The answer is 28. What number did your teacher think of? Slide 145 / 146 A 45 B 5 C 28 D Scott is reading a book that is 50 pages long. Melanie is reading a book with 3 times as many pages. How many pages does Melanie's book have? Select the equation to represent this problem. Slide 146 / 146 A 50 3 = B 50 x 3 = m C 3 x m = 50 Answer D m 50 = 3
Fourth Grade. Multiplication Review. Slide 1 / 146 Slide 2 / 146. Slide 3 / 146. Slide 4 / 146. Slide 5 / 146. Slide 6 / 146
 Slide 1 / 146 Slide 2 / 146 Fourth Grade Multiplication and Division Relationship 2015-11-23 www.njctl.org Multiplication Review Slide 3 / 146 Table of Contents Properties of Multiplication Factors Prime
Slide 1 / 146 Slide 2 / 146 Fourth Grade Multiplication and Division Relationship 2015-11-23 www.njctl.org Multiplication Review Slide 3 / 146 Table of Contents Properties of Multiplication Factors Prime
Busy Ant Maths and the Scottish Curriculum for Excellence Foundation Level - Primary 1
 Busy Ant Maths and the Scottish Curriculum for Excellence Foundation Level - Primary 1 Number, money and measure Estimation and rounding Number and number processes Fractions, decimal fractions and percentages
Busy Ant Maths and the Scottish Curriculum for Excellence Foundation Level - Primary 1 Number, money and measure Estimation and rounding Number and number processes Fractions, decimal fractions and percentages
ARKANSAS DEPARTMENT OF EDUCATION MATHEMATICS ADOPTION. Common Core State Standards Correlation. and
 ARKANSAS DEPARTMENT OF EDUCATION MATHEMATICS ADOPTION 2012 s Correlation and s Comparison with Expectations Correlation ARKANSAS DEPARTMENT OF EDUCATION MATHEMATICS ADOPTION Two Number, Data and Space
ARKANSAS DEPARTMENT OF EDUCATION MATHEMATICS ADOPTION 2012 s Correlation and s Comparison with Expectations Correlation ARKANSAS DEPARTMENT OF EDUCATION MATHEMATICS ADOPTION Two Number, Data and Space
LETTER TO PARENTS SCIENCE NEWS. Dear Parents,
 LETTER TO PARENTS Cut here and paste onto school letterhead before making copies. Dear Parents, SCIENCE NEWS Our class is beginning a new science unit using the FOSS Magnetism and Electricity Module. We
LETTER TO PARENTS Cut here and paste onto school letterhead before making copies. Dear Parents, SCIENCE NEWS Our class is beginning a new science unit using the FOSS Magnetism and Electricity Module. We
Scientific Notation. Slide 1 / 106. Slide 2 / 106. Slide 3 / th Grade. Table of Contents. New Jersey Center for Teaching and Learning
 New Jersey Center for Teaching and Learning Slide 1 / 106 Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
New Jersey Center for Teaching and Learning Slide 1 / 106 Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Grade 3: Houghton Mifflin Math correlated to Riverdeep Destination Math
 1 : correlated to Unit 1 Chapter 1 Uses of Numbers 4A 4B, 4 5 Place Value: Ones, Tens, and Hundreds 6A 6B, 6 7 How Big is One Thousand? 8A 8B, 8 9 Place Value Through Thousands 10A 10B, 10 11, 12 13 Problem-Solving
1 : correlated to Unit 1 Chapter 1 Uses of Numbers 4A 4B, 4 5 Place Value: Ones, Tens, and Hundreds 6A 6B, 6 7 How Big is One Thousand? 8A 8B, 8 9 Place Value Through Thousands 10A 10B, 10 11, 12 13 Problem-Solving
Represent and solve problems involving addition and subtraction. Work with equal groups of objects to gain foundations for multiplication.
 Correlation S T A N D A R D S F O R M A T H E M A T I C A L C O N T E N T This correlation includes Classroom Routines but does not include ongoing review in Daily Practice and Homework. Domain 2.OA Operations
Correlation S T A N D A R D S F O R M A T H E M A T I C A L C O N T E N T This correlation includes Classroom Routines but does not include ongoing review in Daily Practice and Homework. Domain 2.OA Operations
Missouri Learning Standards Grade-Level Expectations - Mathematics
 A Correlation of 2017 To the Missouri Learning Standards - Mathematics Kindergarten Grade 5 Introduction This document demonstrates how Investigations 3 in Number, Data, and Space, 2017, aligns to, Grades
A Correlation of 2017 To the Missouri Learning Standards - Mathematics Kindergarten Grade 5 Introduction This document demonstrates how Investigations 3 in Number, Data, and Space, 2017, aligns to, Grades
Module: Mathematical Reasoning
 Module: Mathematical Reasoning Lesson Title: Speeding Along Objectives and Standards Students will: Determine whether a relationship is a function Calculate the value of a function through a real-world
Module: Mathematical Reasoning Lesson Title: Speeding Along Objectives and Standards Students will: Determine whether a relationship is a function Calculate the value of a function through a real-world
Grade 1: Houghton Mifflin Math correlated to Riverdeep Destination Math
 1 : correlated to Unit 1 Chapter 1 Numbers 0 Through 5 7A 7B, 7 8 Numbers 6 Through 10 9A 9B, 9 10 Order 0 Through 10 11A 11B, 11 12 Compare 0 Through 10 13A 13B, 13 14, 15 16 Numbers 10 Through 15 17A
1 : correlated to Unit 1 Chapter 1 Numbers 0 Through 5 7A 7B, 7 8 Numbers 6 Through 10 9A 9B, 9 10 Order 0 Through 10 11A 11B, 11 12 Compare 0 Through 10 13A 13B, 13 14, 15 16 Numbers 10 Through 15 17A
Houghton Mifflin MATHEMATICS. Level 1 correlated to Chicago Academic Standards and Framework Grade 1
 State Goal 6: Demonstrate and apply a knowledge and sense of numbers, including basic arithmetic operations, number patterns, ratios and proportions. CAS A. Relate counting, grouping, and place-value concepts
State Goal 6: Demonstrate and apply a knowledge and sense of numbers, including basic arithmetic operations, number patterns, ratios and proportions. CAS A. Relate counting, grouping, and place-value concepts
Busy Ant Maths and the Scottish Curriculum for Excellence Year 6: Primary 7
 Busy Ant Maths and the Scottish Curriculum for Excellence Year 6: Primary 7 Number, money and measure Estimation and rounding Number and number processes Including addition, subtraction, multiplication
Busy Ant Maths and the Scottish Curriculum for Excellence Year 6: Primary 7 Number, money and measure Estimation and rounding Number and number processes Including addition, subtraction, multiplication
Problem Solving Recording Sheet
 Problem Solving Recording Sheet 1 Problem: MAKE SENSE OF THE PROBLEM Need to Find Given PERSEVERE IN SOLVING THE PROBLEM Some Ways to Represent Problems Draw a Picture Make a Bar Diagram Make a Table or
Problem Solving Recording Sheet 1 Problem: MAKE SENSE OF THE PROBLEM Need to Find Given PERSEVERE IN SOLVING THE PROBLEM Some Ways to Represent Problems Draw a Picture Make a Bar Diagram Make a Table or
Simple Gears and Transmission
 Simple Gears and Transmission Simple Gears and Transmission page: of 4 How can transmissions be designed so that they provide the force, speed and direction required and how efficient will the design be?
Simple Gears and Transmission Simple Gears and Transmission page: of 4 How can transmissions be designed so that they provide the force, speed and direction required and how efficient will the design be?
Correlation to the New York Common Core Learning Standards for Mathematics, Grade 1
 Correlation to the New York Common Core Learning Standards for Mathematics, Grade 1 Math Expressions Common Core 2013 Grade 1 Houghton Mifflin Harcourt Publishing Company. All rights reserved. Printed
Correlation to the New York Common Core Learning Standards for Mathematics, Grade 1 Math Expressions Common Core 2013 Grade 1 Houghton Mifflin Harcourt Publishing Company. All rights reserved. Printed
Scientific Notation. Slide 1 / 106. Slide 2 / 106. Slide 4 / 106. Slide 3 / 106. Slide 5 / 106. Slide 6 / th Grade.
 Slide 1 / 106 New Jersey enter for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Slide 1 / 106 New Jersey enter for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Objective: Estimate and measure liquid volume in liters and milliliters using the vertical number line.
 Lesson 10 Objective: Estimate and measure liquid volume in liters and milliliters using the Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief Total Time
Lesson 10 Objective: Estimate and measure liquid volume in liters and milliliters using the Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief Total Time
Correlation to the New York Common Core Learning Standards for Mathematics, Grade K
 Correlation to the New York Common Core Learning Standards for Mathematics, Grade K Math Expressions Common Core 2013 Grade K Houghton Mifflin Harcourt Publishing Company. All rights reserved. Printed
Correlation to the New York Common Core Learning Standards for Mathematics, Grade K Math Expressions Common Core 2013 Grade K Houghton Mifflin Harcourt Publishing Company. All rights reserved. Printed
Correlation to the Common Core State Standards
 Correlation to the Common Core State Standards Go Math! 2011 Grade 3 Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Correlation to the Common Core State Standards Go Math! 2011 Grade 3 Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Chapter Review Problems
 Chapter Review Problems Unit 1.1 Reading, writing, and rounding numbers Change these numbers to words: 1. 317 Three hundred seventeen 2. 8,257,116 Eight million, two hundred fifty-seven thousand, one hundred
Chapter Review Problems Unit 1.1 Reading, writing, and rounding numbers Change these numbers to words: 1. 317 Three hundred seventeen 2. 8,257,116 Eight million, two hundred fifty-seven thousand, one hundred
Chapter 2: Approaches to Problem Solving Lecture notes Math 1030 Section A
 Section A.1: You Can t Add Apples and Oranges Definition of units The units of a quantity describe what is measured or counted. We cannot add or subtract numbers with different units, but we can multiply
Section A.1: You Can t Add Apples and Oranges Definition of units The units of a quantity describe what is measured or counted. We cannot add or subtract numbers with different units, but we can multiply
Orientation and Conferencing Plan Stage 1
 Orientation and Conferencing Plan Stage 1 Orientation Ensure that you have read about using the plan in the Program Guide. Book summary Read the following summary to the student. Everyone plays with the
Orientation and Conferencing Plan Stage 1 Orientation Ensure that you have read about using the plan in the Program Guide. Book summary Read the following summary to the student. Everyone plays with the
Correlation to the. Common Core State Standards. Go Math! 2011 Grade K
 Correlation to the Common Core State Standards Go Math! 2011 Grade K Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Correlation to the Common Core State Standards Go Math! 2011 Grade K Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Objective: Estimate and measure liquid volume in liters and milliliters using the vertical number line.
 Lesson 10 Objective: Estimate and measure liquid volume in liters and milliliters using the Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief Total Time
Lesson 10 Objective: Estimate and measure liquid volume in liters and milliliters using the Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief Total Time
Correlation S T A N D A R D S F O R M A T H E M A T I C A L C O N T E N T. Know number names and the count sequence.
 Correlation S T A N D A R D S F O R M A T H E M A T I C A L C O N T E N T This correlation includes Classroom Routines but does not include ongoing review in Daily Practice and Homework. Domain K.CC Counting
Correlation S T A N D A R D S F O R M A T H E M A T I C A L C O N T E N T This correlation includes Classroom Routines but does not include ongoing review in Daily Practice and Homework. Domain K.CC Counting
11.1 CURRENT ELECTRICITY. Electrochemical Cells (the energy source) pg Wet Cell. Dry Cell. Positive. Terminal. Negative.
 Date: SNC1D: Electricity 11.1 CURRENT ELECTRICITY Define: CIRCUIT: path that electrons follow. CURRENT ELECTRICITY: continuous flow of electrons in a circuit LOAD: device that converts electrical energy
Date: SNC1D: Electricity 11.1 CURRENT ELECTRICITY Define: CIRCUIT: path that electrons follow. CURRENT ELECTRICITY: continuous flow of electrons in a circuit LOAD: device that converts electrical energy
Name Period. (c) Now replace the round bulb(s) with long bulb(s). How does the brightness change?
 Name Period P Phys 1 Discovery Lesson Electric Circuits 2.1 Experiment: Charge Flow Strength & Resistors circuit is an unbroken loop of conductors. Charge (q) can flow continuously in a circuit. If an
Name Period P Phys 1 Discovery Lesson Electric Circuits 2.1 Experiment: Charge Flow Strength & Resistors circuit is an unbroken loop of conductors. Charge (q) can flow continuously in a circuit. If an
Car Comparison Project
 NAME Car Comparison Project Introduction Systems of linear equations are a useful way to solve common problems in different areas of life. One of the most powerful ways to use them is in a comparison model
NAME Car Comparison Project Introduction Systems of linear equations are a useful way to solve common problems in different areas of life. One of the most powerful ways to use them is in a comparison model
CC COURSE 1 ETOOLS - T
 CC COURSE 1 ETOOLS - T Table of Contents General etools... 5 Algebra Tiles (CPM)... 6 Pattern Tile & Dot Tool (CPM)... 9 Area and Perimeter (CPM)...11 Base Ten Blocks (CPM)...14 +/- Tiles & Number Lines
CC COURSE 1 ETOOLS - T Table of Contents General etools... 5 Algebra Tiles (CPM)... 6 Pattern Tile & Dot Tool (CPM)... 9 Area and Perimeter (CPM)...11 Base Ten Blocks (CPM)...14 +/- Tiles & Number Lines
Use the graph to answer the question. Write the correct letter in the blank. Dave had 7 oranges. He juiced oranges. How many oranges are left?
 1 Use the graph to answer the question. 4 High Temperature ( F) 120 1 0 90 80 70 60 50 40 30 20 0 Temperature Over a Week Sunday Monday Tuesday Wednesday Thursday Friday Saturday Dave had 7 oranges. He
1 Use the graph to answer the question. 4 High Temperature ( F) 120 1 0 90 80 70 60 50 40 30 20 0 Temperature Over a Week Sunday Monday Tuesday Wednesday Thursday Friday Saturday Dave had 7 oranges. He
News English.com Ready-to-use ESL / EFL Lessons Barack Obama s supercar shown to the world
 www.breaking News English.com Ready-to-use ESL / EFL Lessons 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS The Breaking News English.com Resource Book http://www.breakingnewsenglish.com/book.html Barack
www.breaking News English.com Ready-to-use ESL / EFL Lessons 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS The Breaking News English.com Resource Book http://www.breakingnewsenglish.com/book.html Barack
5-3 Complex Fractions and Unit Rates
 Simplify. 1. 2. esolutions Manual - Powered by Cognero Page 1 3. 4. 5. esolutions Manual - Powered by Cognero Page 2 6. 7. Monica reads pages of a mystery book in 9 minutes. What is her average reading
Simplify. 1. 2. esolutions Manual - Powered by Cognero Page 1 3. 4. 5. esolutions Manual - Powered by Cognero Page 2 6. 7. Monica reads pages of a mystery book in 9 minutes. What is her average reading
U-Score U-Score AAC Rank AAC Rank Vocabulary Vocabulary
 go 1 927 you 2 7600 i 3 4443 more 4 2160 help 5 659 it 6 9386 want 7 586 in 8 19004 that 9 10184 like 10 1810 what 11 2560 make 12 1264 is 13 10257 on 14 6674 out 15 2350 do 16 2102 here 17 655 eat 18
go 1 927 you 2 7600 i 3 4443 more 4 2160 help 5 659 it 6 9386 want 7 586 in 8 19004 that 9 10184 like 10 1810 what 11 2560 make 12 1264 is 13 10257 on 14 6674 out 15 2350 do 16 2102 here 17 655 eat 18
Problem of the Month. Movin n Groovin
 Problem of the Month Movin n Groovin Level A: Maria and Tran each have a pet hamster. They have a maze for the hamsters to run through. Maria says she thinks her hamster can run through the maze faster
Problem of the Month Movin n Groovin Level A: Maria and Tran each have a pet hamster. They have a maze for the hamsters to run through. Maria says she thinks her hamster can run through the maze faster
Car Comparison Project
 NAME Car Comparison Project Introduction Systems of linear equations are a useful way to solve common problems in different areas of life. One of the most powerful ways to use them is in a comparison model
NAME Car Comparison Project Introduction Systems of linear equations are a useful way to solve common problems in different areas of life. One of the most powerful ways to use them is in a comparison model
NEW CAR TIPS. Teaching Guidelines
 NEW CAR TIPS Teaching Guidelines Subject: Algebra Topics: Patterns and Functions Grades: 7-12 Concepts: Independent and dependent variables Slope Direct variation (optional) Knowledge and Skills: Can relate
NEW CAR TIPS Teaching Guidelines Subject: Algebra Topics: Patterns and Functions Grades: 7-12 Concepts: Independent and dependent variables Slope Direct variation (optional) Knowledge and Skills: Can relate
Porsche unveils 4-door sports car
 www.breaking News English.com Ready-to-use ESL / EFL Lessons Porsche unveils 4-door sports car URL: http://www.breakingnewsenglish.com/0507/050728-porsche-e.html Today s contents The Article 2 Warm-ups
www.breaking News English.com Ready-to-use ESL / EFL Lessons Porsche unveils 4-door sports car URL: http://www.breakingnewsenglish.com/0507/050728-porsche-e.html Today s contents The Article 2 Warm-ups
1.2 Flipping Ferraris
 1.2 Flipping Ferraris A Solidify Understanding Task When people first learn to drive, they are often told that the faster they are driving, the longer it will take to stop. So, when you re driving on the
1.2 Flipping Ferraris A Solidify Understanding Task When people first learn to drive, they are often told that the faster they are driving, the longer it will take to stop. So, when you re driving on the
1. (s r r d v i e) These people work on buses or in taxis. They are. 2. (s s s g p n r a e e) These people ride on public transportation.
 10.1 PUBLIC TRANSPORTATION 1 What s There? Circle the answers to the questions. What can you find... DICTIONARY PAGE 71 1.... inside a train station? trains tracks taxis 2.... inside a subway station?
10.1 PUBLIC TRANSPORTATION 1 What s There? Circle the answers to the questions. What can you find... DICTIONARY PAGE 71 1.... inside a train station? trains tracks taxis 2.... inside a subway station?
PHY152H1S Practical 3: Introduction to Circuits
 PHY152H1S Practical 3: Introduction to Circuits Don t forget: List the NAMES of all participants on the first page of each day s write-up. Note if any participants arrived late or left early. Put the DATE
PHY152H1S Practical 3: Introduction to Circuits Don t forget: List the NAMES of all participants on the first page of each day s write-up. Note if any participants arrived late or left early. Put the DATE
Name Date Period. MATERIALS: Light bulb Battery Wires (2) Light socket Switch Penny
 Name Date Period Lab: Electricity and Circuits CHAPTER 34: CURRENT ELECTRICITY BACKGROUND: Just as water is the flow of H 2 O molecules, electric current is the flow of charged particles. In circuits of
Name Date Period Lab: Electricity and Circuits CHAPTER 34: CURRENT ELECTRICITY BACKGROUND: Just as water is the flow of H 2 O molecules, electric current is the flow of charged particles. In circuits of
Unit 1 Chapter 3 Factors and Products
 Unit 1 Chapter 3 Factors and Products By the end of this unit, I should be able to Write a number as a product of its prime factors Explain why 0 and 1 have no prime factors Use prime factorization to:
Unit 1 Chapter 3 Factors and Products By the end of this unit, I should be able to Write a number as a product of its prime factors Explain why 0 and 1 have no prime factors Use prime factorization to:
Rated MPG for Confusion: Using Gas Mileage to Learn Graphing and Data Analysis
 Rated MPG for Confusion: Using Gas Mileage to Learn Graphing and Data Analysis by Claudia Bode, Center for Environmentally Beneficial Catalysis, University of Kansas, Lawrence, KS Alan Gleue, Science Department,
Rated MPG for Confusion: Using Gas Mileage to Learn Graphing and Data Analysis by Claudia Bode, Center for Environmentally Beneficial Catalysis, University of Kansas, Lawrence, KS Alan Gleue, Science Department,
Linear Modeling Exercises. In case you d like to see why the best fit line is also called a least squares regression line here ya go!
 Linear Modeling Exercises Pages 308 311 Problems 1 4, 5-9 (you might want to do the E exercises next), 20 In case you d like to see why the best fit line is also called a least squares regression line
Linear Modeling Exercises Pages 308 311 Problems 1 4, 5-9 (you might want to do the E exercises next), 20 In case you d like to see why the best fit line is also called a least squares regression line
Algebra 1 Predicting Patterns & Examining Experiments. Unit 2: Maintaining Balance Section 1: Balance with Addition
 Algebra 1 Predicting Patterns & Examining Experiments Unit 2: Maintaining Balance Section 1: Balance with Addition What is the weight ratio of basketballs to softballs? (Partner Discussion) Have students
Algebra 1 Predicting Patterns & Examining Experiments Unit 2: Maintaining Balance Section 1: Balance with Addition What is the weight ratio of basketballs to softballs? (Partner Discussion) Have students
Mandatory Experiment: Electric conduction
 Name: Class: Mandatory Experiment: Electric conduction In this experiment, you will investigate how different materials affect the brightness of a bulb in a simple electric circuit. 1. Take a battery holder,
Name: Class: Mandatory Experiment: Electric conduction In this experiment, you will investigate how different materials affect the brightness of a bulb in a simple electric circuit. 1. Take a battery holder,
MiSTE STEM Camp Solar Lesson July, 2016 Standard(s) Learning targets Assessment Essential vocabulary. Informal - Discussion and participation
 MiSTE STEM Camp Solar Lesson July, 2016 Standard(s) Learning targets Assessment Essential vocabulary Science SEPS.1 - I can clarify problems to determine criteria for possible solutions. Science SEPS.8
MiSTE STEM Camp Solar Lesson July, 2016 Standard(s) Learning targets Assessment Essential vocabulary Science SEPS.1 - I can clarify problems to determine criteria for possible solutions. Science SEPS.8
ALIGNING A 2007 CADILLAC CTS-V
 ALIGNING A 2007 CADILLAC CTS-V I ll describe a four-wheel alignment of a 2007 Cadillac CTS-V in this document using homemade alignment tools. I described the tools in a previous document. The alignment
ALIGNING A 2007 CADILLAC CTS-V I ll describe a four-wheel alignment of a 2007 Cadillac CTS-V in this document using homemade alignment tools. I described the tools in a previous document. The alignment
Deriving Consistency from LEGOs
 Deriving Consistency from LEGOs What we have learned in 6 years of FLL by Austin and Travis Schuh Objectives Basic Building Techniques How to Build Arms and Drive Trains Using Sensors How to Choose a Programming
Deriving Consistency from LEGOs What we have learned in 6 years of FLL by Austin and Travis Schuh Objectives Basic Building Techniques How to Build Arms and Drive Trains Using Sensors How to Choose a Programming
Cub Scout Den Meeting Outline
 Cub Scout Den Meeting Outline Month: August Week: 2 Point of the Scout Law: Clean Before the Meeting Gathering Opening Activity Games Business items/take home Closing After the meeting Tiger Wolf Bear
Cub Scout Den Meeting Outline Month: August Week: 2 Point of the Scout Law: Clean Before the Meeting Gathering Opening Activity Games Business items/take home Closing After the meeting Tiger Wolf Bear
1. What are some everyday examples (that are NOT listed above) in which you use torque to complete a task?
 ID: NAME: DATE: CLASS: Chapter 11: Torque Notes POGIL #1 REMEMBER: Throughout this paper, you will see some symbols. The stop sign means STOP and check with a teacher before continuing. The key means THIS
ID: NAME: DATE: CLASS: Chapter 11: Torque Notes POGIL #1 REMEMBER: Throughout this paper, you will see some symbols. The stop sign means STOP and check with a teacher before continuing. The key means THIS
News English.com Ready-to-use ESL / EFL Lessons
 www.breaking News English.com Ready-to-use ESL / EFL Lessons 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS The Breaking News English.com Resource Book http://www.breakingnewsenglish.com/book.html Japanese
www.breaking News English.com Ready-to-use ESL / EFL Lessons 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS The Breaking News English.com Resource Book http://www.breakingnewsenglish.com/book.html Japanese
Physics 2048 Test 2 Dr. Jeff Saul Fall 2001
 Physics 2048 Test 2 Dr. Jeff Saul Fall 2001 Name: Group: Date: READ THESE INSTRUCTIONS BEFORE YOU BEGIN Before you start the test, WRITE YOUR NAME ON EVERY PAGE OF THE EXAM. Calculators are permitted,
Physics 2048 Test 2 Dr. Jeff Saul Fall 2001 Name: Group: Date: READ THESE INSTRUCTIONS BEFORE YOU BEGIN Before you start the test, WRITE YOUR NAME ON EVERY PAGE OF THE EXAM. Calculators are permitted,
Getting a Car J. Folta
 Getting a Car Getting a Car J. Folta As the head of a family, I have many decisions to make about how my husband and I spend our money. We need to figure out the way to get the most out of what we make
Getting a Car Getting a Car J. Folta As the head of a family, I have many decisions to make about how my husband and I spend our money. We need to figure out the way to get the most out of what we make
GRADE 7 TEKS ALIGNMENT CHART
 GRADE 7 TEKS ALIGNMENT CHART TEKS 7.2 extend previous knowledge of sets and subsets using a visual representation to describe relationships between sets of rational numbers. 7.3.A add, subtract, multiply,
GRADE 7 TEKS ALIGNMENT CHART TEKS 7.2 extend previous knowledge of sets and subsets using a visual representation to describe relationships between sets of rational numbers. 7.3.A add, subtract, multiply,
Electricity. Grade: 1 st grade Category: Physical Science NGSS: ETS1.A: Defining and Delimiting Engineering Problems
 Electricity Grade: 1 st grade Category: Physical Science NGSS: ETS1.A: Defining and Delimiting Engineering Problems Description: In this lesson, the students will learn that some objects need electricity
Electricity Grade: 1 st grade Category: Physical Science NGSS: ETS1.A: Defining and Delimiting Engineering Problems Description: In this lesson, the students will learn that some objects need electricity
Smart Spinner. Age 7+ Teacher s Notes. In collaboration with NASA
 Smart Spinner Age 7+ Teacher s Notes In collaboration with NASA LEGO and the LEGO logo are trademarks of the/sont des marques de commerce de/son marcas registradas de LEGO Group. 2012 The LEGO Group. 190912
Smart Spinner Age 7+ Teacher s Notes In collaboration with NASA LEGO and the LEGO logo are trademarks of the/sont des marques de commerce de/son marcas registradas de LEGO Group. 2012 The LEGO Group. 190912
IT'S MAGNETIC (1 Hour)
 IT'S MAGNETIC (1 Hour) Addresses NGSS Level of Difficulty: 4 Grade Range: 3-5 OVERVIEW In this activity, students will create a simple electromagnet using a nail, a battery, and copper wire. They will
IT'S MAGNETIC (1 Hour) Addresses NGSS Level of Difficulty: 4 Grade Range: 3-5 OVERVIEW In this activity, students will create a simple electromagnet using a nail, a battery, and copper wire. They will
Every Friday, Bart and Lisa meet their friends at an after-school club. They spend the afternoon playing Power Up, a game about batteries.
 Battery Lab NAME Every Friday, Bart and Lisa meet their friends at an after-school club. They spend the afternoon playing Power Up, a game about batteries. The object of the game is to arrange battery
Battery Lab NAME Every Friday, Bart and Lisa meet their friends at an after-school club. They spend the afternoon playing Power Up, a game about batteries. The object of the game is to arrange battery
Video Communications Presents. Reference Guide and Test Questions. Tail Swing Safety for School Bus Drivers
 Video Communications Presents Reference Guide and Test Questions Tail Swing Safety for School Bus Drivers Introduction Tail swing occurs whenever a bus makes a turn. The school bus driver must be aware
Video Communications Presents Reference Guide and Test Questions Tail Swing Safety for School Bus Drivers Introduction Tail swing occurs whenever a bus makes a turn. The school bus driver must be aware
Your web browser (Safari 7) is out of date. For more security, comfort and. the best experience on this site: Update your browser Ignore
 Your web browser (Safari 7) is out of date. For more security, comfort and Activitydevelop the best experience on this site: Update your browser Ignore Circuits with Friends What is a circuit, and what
Your web browser (Safari 7) is out of date. For more security, comfort and Activitydevelop the best experience on this site: Update your browser Ignore Circuits with Friends What is a circuit, and what
What Is Analysis? Rebecca Jarvis, Ph.D., and Ginger, Ca.T., Eastern Arizona College
 What Is Analysis? Rebecca Jarvis, Ph.D., and Ginger, Ca.T., Eastern Arizona College My desk at home What s on the table Let s list everything that is on the table: two laptops, one opened and one closed;
What Is Analysis? Rebecca Jarvis, Ph.D., and Ginger, Ca.T., Eastern Arizona College My desk at home What s on the table Let s list everything that is on the table: two laptops, one opened and one closed;
C67_2_27_Investigation 5. February 27, Rewrite in slope intercept form. Homework: Page 78, 2 Page 80, 13 & 14
 Find ten possible car miles, SUV miles pairs that give a total of no more than 1,000 miles. One month the family drove the car 500 miles and the SUV 500 miles. Was the total for this month no more than
Find ten possible car miles, SUV miles pairs that give a total of no more than 1,000 miles. One month the family drove the car 500 miles and the SUV 500 miles. Was the total for this month no more than
correlated to the Virginia Standards of Learning, Grade 6
 correlated to the Virginia Standards of Learning, Grade 6 Standards to Content Report McDougal Littell Math, Course 1 2007 correlated to the Virginia Standards of Standards: Virginia Standards of Number
correlated to the Virginia Standards of Learning, Grade 6 Standards to Content Report McDougal Littell Math, Course 1 2007 correlated to the Virginia Standards of Standards: Virginia Standards of Number
ANSWERS m 4. The man takes an empty vessel other than these.
 BRAIN-TEASERS 1. From a basket of mangoes when counted in twos there was one extra, counted in threes there were two extra, counted in fours there were three extra, counted in fives there were four extra,
BRAIN-TEASERS 1. From a basket of mangoes when counted in twos there was one extra, counted in threes there were two extra, counted in fours there were three extra, counted in fives there were four extra,
3-2 Estimate Products. Estimate the product SOLUTION: Use rounding. So, is about SOLUTION: Use rounding.
 Estimate the product. 1. 9.7 3.3 So, 9.7 3.3 is about 30. 2. 3.4 5.6 So, 3.4 5.6 is about 18. 3. 17.5 8.4 So, 17.5 8.4 is about 160. 4. 44.8 5.1 225 So, 44.8 5.1 is about 225. 5. 28.21 8.02 So, 28.21 8.02
Estimate the product. 1. 9.7 3.3 So, 9.7 3.3 is about 30. 2. 3.4 5.6 So, 3.4 5.6 is about 18. 3. 17.5 8.4 So, 17.5 8.4 is about 160. 4. 44.8 5.1 225 So, 44.8 5.1 is about 225. 5. 28.21 8.02 So, 28.21 8.02
Simple Gears and Transmission
 Simple Gears and Transmission Contents How can transmissions be designed so that they provide the force, speed and direction required and how efficient will the design be? Initial Problem Statement 2 Narrative
Simple Gears and Transmission Contents How can transmissions be designed so that they provide the force, speed and direction required and how efficient will the design be? Initial Problem Statement 2 Narrative
Mechanical Systems. Section 1.0 Machines are tools that help humans do work. 1.1 Simple Machines- Meeting Human Needs Water Systems
 Unit 4 Mechanical Systems Section 1.0 Machines are tools that help humans do work. Define: machine- 1.1 Simple Machines- Meeting Human Needs Water Systems Then: Now: The earliest devices were devices.
Unit 4 Mechanical Systems Section 1.0 Machines are tools that help humans do work. Define: machine- 1.1 Simple Machines- Meeting Human Needs Water Systems Then: Now: The earliest devices were devices.
Cub Scout Den Meeting Outline
 Cub Scout Den Meeting Outline Month: July Week: 1 Point of the Scout Law: Loyal Before the Meeting Gathering Opening Games Activity Business items/take home Closing After the meeting Tiger Wolf Bear Webelos
Cub Scout Den Meeting Outline Month: July Week: 1 Point of the Scout Law: Loyal Before the Meeting Gathering Opening Games Activity Business items/take home Closing After the meeting Tiger Wolf Bear Webelos
LETTER TO FAMILY. Science News. Cut here and glue letter onto school letterhead before making copies.
 LETTER TO FAMILY Cut here and glue letter onto school letterhead before making copies. Science News Dear Family, Our class is beginning a new science unit using the. We will investigate energy, build electric
LETTER TO FAMILY Cut here and glue letter onto school letterhead before making copies. Science News Dear Family, Our class is beginning a new science unit using the. We will investigate energy, build electric
ELECTRICITY: ELECTROMAGNETISM QUESTIONS
 ELECTRICITY: ELECTROMAGNETISM QUESTIONS The flying fox (2017;3) Sam has a flying fox (zip line) that he wants to use in the dark. Sam connects a 12.0 V battery to a spotlight, using two 1.60-metre-long
ELECTRICITY: ELECTROMAGNETISM QUESTIONS The flying fox (2017;3) Sam has a flying fox (zip line) that he wants to use in the dark. Sam connects a 12.0 V battery to a spotlight, using two 1.60-metre-long
Level 5-8 Little Lord Fauntleroy
 Level 5-8 Little Lord Fauntleroy Workbook Teacher s Guide and Answer Key A. Summary 1. Book Summary Teacher s Guide Cedric was a kind seven-year-old boy. He was born in America, but his father was from
Level 5-8 Little Lord Fauntleroy Workbook Teacher s Guide and Answer Key A. Summary 1. Book Summary Teacher s Guide Cedric was a kind seven-year-old boy. He was born in America, but his father was from
Stopping distance = thinking distance + braking distance.
 Q1. (a) A driver may have to make an emergency stop. Stopping distance = thinking distance + braking distance. Give three different factors which affect the thinking distance or the braking distance. In
Q1. (a) A driver may have to make an emergency stop. Stopping distance = thinking distance + braking distance. Give three different factors which affect the thinking distance or the braking distance. In
ACTIVITY 1: Electric Circuit Interactions
 CYCLE 5 Developing Ideas ACTIVITY 1: Electric Circuit Interactions Purpose Many practical devices work because of electricity. In this first activity of the Cycle you will first focus your attention on
CYCLE 5 Developing Ideas ACTIVITY 1: Electric Circuit Interactions Purpose Many practical devices work because of electricity. In this first activity of the Cycle you will first focus your attention on
units edition imperial PSI & lbs/in2 Name
 L R E W O P D I FLU Name Set: imperial units edition PSI & lbs/in2 This lab will provide you an understanding of: Hydraulic Systems Pneumatic Systems Cylinders Pascal s Law Liquids & Gases Pressure Kinetic
L R E W O P D I FLU Name Set: imperial units edition PSI & lbs/in2 This lab will provide you an understanding of: Hydraulic Systems Pneumatic Systems Cylinders Pascal s Law Liquids & Gases Pressure Kinetic
Chapter 7: DC Motors and Transmissions. 7.1: Basic Definitions and Concepts
 Chapter 7: DC Motors and Transmissions Electric motors are one of the most common types of actuators found in robotics. Using them effectively will allow your robot to take action based on the direction
Chapter 7: DC Motors and Transmissions Electric motors are one of the most common types of actuators found in robotics. Using them effectively will allow your robot to take action based on the direction
Scholastic Big Day for PreK. Arkansas Early Childhood Education Framework for Three & Four Year Old Children 2011
 Scholastic Big Day for PreK Correlated to the Arkansas Early Childhood Education Framework for Three & Four Year Old Children 2011 TM & Scholastic Inc. All rights reserved. SCHOLASTIC, Big Day for PreK,
Scholastic Big Day for PreK Correlated to the Arkansas Early Childhood Education Framework for Three & Four Year Old Children 2011 TM & Scholastic Inc. All rights reserved. SCHOLASTIC, Big Day for PreK,
SCIENCE 8. Unit 4 Booklet. Machines and Mechanical Systems
 SCIENCE 8 Unit 4 Booklet Machines and Mechanical Systems TOPIC 1 REINFORCEMENT Levers Have Class BLM 4-2 Goal Identify items as Class 1, Class 2, or Class 3 levers. Introduction There are three classes
SCIENCE 8 Unit 4 Booklet Machines and Mechanical Systems TOPIC 1 REINFORCEMENT Levers Have Class BLM 4-2 Goal Identify items as Class 1, Class 2, or Class 3 levers. Introduction There are three classes
Name: Period: Due Date: Physics Project: Balloon Powered Car
 Name: Period: Due Date: Physics Project: Balloon Powered Car Challenge: Design and build a balloon car that will travel the greatest distance in the Balloon Car Cup. To do this, you must combine key concepts
Name: Period: Due Date: Physics Project: Balloon Powered Car Challenge: Design and build a balloon car that will travel the greatest distance in the Balloon Car Cup. To do this, you must combine key concepts
Scholastic s Early Childhood Program Correlated to the Minnesota Pre-K Standards
 Scholastic s Early Childhood Program 5/2/07 Page 1 DOMAIN I: EMOTIONAL AND SOCIAL DEVELOPMENT EMOTIONAL DEVELOPMENT 2. 3. 4. 5. Demonstrate increasing competency in recognizing and describing own emotions
Scholastic s Early Childhood Program 5/2/07 Page 1 DOMAIN I: EMOTIONAL AND SOCIAL DEVELOPMENT EMOTIONAL DEVELOPMENT 2. 3. 4. 5. Demonstrate increasing competency in recognizing and describing own emotions
Compound Gears Laboratory - Part 2
 Compound Gears Laboratory - Part 2 Names: Date: About this Laboratory In this laboratory, you will explore compound gear trains, gear ratios, and how the number of teeth on a drive and driven gear affect
Compound Gears Laboratory - Part 2 Names: Date: About this Laboratory In this laboratory, you will explore compound gear trains, gear ratios, and how the number of teeth on a drive and driven gear affect
Please print legibly. Names
 SCORE Please print legibly School / Team Names Directions: Answers must be left in one of the following forms: 1. Integer (example: 7) 2. Simplified fraction (example:!! ) 3. Mixed number, fraction part
SCORE Please print legibly School / Team Names Directions: Answers must be left in one of the following forms: 1. Integer (example: 7) 2. Simplified fraction (example:!! ) 3. Mixed number, fraction part
Electricity and Magnetism
 Electricity and Magnetism Electric Current and Electric Circuits What do you think? Read the statement below and decide whether you agree or disagree with it. Place an A in the Before column if you agree
Electricity and Magnetism Electric Current and Electric Circuits What do you think? Read the statement below and decide whether you agree or disagree with it. Place an A in the Before column if you agree
The fractions 2_ 4, 3_
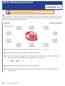 Rate Problem solving Lesson 2.4 5 The fractions 2_ 4, 3_ 6, 4_ 8, and 10 can be written in simplest form as 1_ 2. These are examples of equivalent fractions. Equivalent fractions are fractions with the
Rate Problem solving Lesson 2.4 5 The fractions 2_ 4, 3_ 6, 4_ 8, and 10 can be written in simplest form as 1_ 2. These are examples of equivalent fractions. Equivalent fractions are fractions with the
Index. Calculator, 56, 64, 69, 135, 353 Calendars, 348, 356, 357, 364, 371, 381 Card game, NEL Index
 Index A Acute angle, 94 Adding decimal numbers, 47, 48 fractions, 210 213, 237 239, 241 integers, 310 322 mixed numbers, 245 248 Addition statement, 246, 248 Airport design, 88, 93, 99, 107, 121, 125 Analysing
Index A Acute angle, 94 Adding decimal numbers, 47, 48 fractions, 210 213, 237 239, 241 integers, 310 322 mixed numbers, 245 248 Addition statement, 246, 248 Airport design, 88, 93, 99, 107, 121, 125 Analysing
ECOKIDS BATTERY BUSTERS AUDIT
 DID YOU KNOW Most families have over 2 battery-powered devices at home. That adds up to a whole lot of batteries! Find out how many batteries your family uses by doing a battery audit. TIP 1: DON T MISS
DID YOU KNOW Most families have over 2 battery-powered devices at home. That adds up to a whole lot of batteries! Find out how many batteries your family uses by doing a battery audit. TIP 1: DON T MISS
Electrical Principles & Technologies Topic 3.3-Measuring Energy Input and Output
 Electrical Principles & Technologies Topic 3.3-Measuring Energy Input and Output Page 332-342 Name: Power 1. A Scottish inventor James Watt who invented the steam engine did a tremendous amount of work
Electrical Principles & Technologies Topic 3.3-Measuring Energy Input and Output Page 332-342 Name: Power 1. A Scottish inventor James Watt who invented the steam engine did a tremendous amount of work
Disco 3 Clock Spring / Rotary Coupler replacement
 Disco 3 Clock Spring / Rotary Coupler replacement I recently had to change my Clock spring and thought some folks may find it helpful to see what it entailed. I did lots of reading around but couldn t
Disco 3 Clock Spring / Rotary Coupler replacement I recently had to change my Clock spring and thought some folks may find it helpful to see what it entailed. I did lots of reading around but couldn t
LET S ARGUE: STUDENT WORK PAMELA RAWSON. Baxter Academy for Technology & Science Portland, rawsonmath.
 LET S ARGUE: STUDENT WORK PAMELA RAWSON Baxter Academy for Technology & Science Portland, Maine pamela.rawson@gmail.com @rawsonmath rawsonmath.com Contents Student Movie Data Claims (Cycle 1)... 2 Student
LET S ARGUE: STUDENT WORK PAMELA RAWSON Baxter Academy for Technology & Science Portland, Maine pamela.rawson@gmail.com @rawsonmath rawsonmath.com Contents Student Movie Data Claims (Cycle 1)... 2 Student
(b) Ans. (b) Do these in your notebook using Bela s method: (a) Ans.
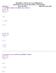 KENDRIYA VIDYALAYA,GANDHIGRAM CHAPTER-13(WAYS OF MULTIPLY AND DIVIDE) CLASS: V SUB: MATHS MONTH: JANUARY 1. Use Bela s method to multiply these numbers. (a) 32 46 Ans. (a)3 2 4 6 1 9 2 + 1 2 8 0 1 4 7
KENDRIYA VIDYALAYA,GANDHIGRAM CHAPTER-13(WAYS OF MULTIPLY AND DIVIDE) CLASS: V SUB: MATHS MONTH: JANUARY 1. Use Bela s method to multiply these numbers. (a) 32 46 Ans. (a)3 2 4 6 1 9 2 + 1 2 8 0 1 4 7
ELECTRIC CURRENT. Name(s)
 Name(s) ELECTRIC CURRT The primary purpose of this activity is to decide upon a model for electric current. As is the case for all scientific models, your electricity model should be able to explain observed
Name(s) ELECTRIC CURRT The primary purpose of this activity is to decide upon a model for electric current. As is the case for all scientific models, your electricity model should be able to explain observed
CH 65 MOTION PROBLEMS, PART 1
 CH 65 MOTION PROBLEMS, PART 1 585 Introduction W hether it s the police pursuing a bank robber, or a physicist determining the velocity of a proton in a linear accelerator, the concepts of time, distance,
CH 65 MOTION PROBLEMS, PART 1 585 Introduction W hether it s the police pursuing a bank robber, or a physicist determining the velocity of a proton in a linear accelerator, the concepts of time, distance,
INVESTIGATION ONE: WHAT DOES A VOLTMETER DO? How Are Values of Circuit Variables Measured?
 How Are Values of Circuit Variables Measured? INTRODUCTION People who use electric circuits for practical purposes often need to measure quantitative values of electric pressure difference and flow rate
How Are Values of Circuit Variables Measured? INTRODUCTION People who use electric circuits for practical purposes often need to measure quantitative values of electric pressure difference and flow rate
 www.newsflashenglish.com The 4 page 60 minute ESL British English lesson 30/03/15 Today, let s talk about driverless cars. Would you go in one? Moreover, would you feel safe in one? The subject is hopefully
www.newsflashenglish.com The 4 page 60 minute ESL British English lesson 30/03/15 Today, let s talk about driverless cars. Would you go in one? Moreover, would you feel safe in one? The subject is hopefully
Science Test Revision
 John Buchan Middle School Science Test Revision 4F Circuits and Conductors 39 min 38 marks Name John Buchan Middle School 1 Level 3 1. Conducting electricity (a) Year 6 are testing objects to see if they
John Buchan Middle School Science Test Revision 4F Circuits and Conductors 39 min 38 marks Name John Buchan Middle School 1 Level 3 1. Conducting electricity (a) Year 6 are testing objects to see if they
Fig 1 An illustration of a spring damper unit with a bell crank.
 The Damper Workbook Over the last couple of months a number of readers and colleagues have been talking to me and asking questions about damping. In particular what has been cropping up has been the mechanics
The Damper Workbook Over the last couple of months a number of readers and colleagues have been talking to me and asking questions about damping. In particular what has been cropping up has been the mechanics
1. (3) My faucet runs at a rate of 5 gallons a minute. How many gallons a second is that?
 Math 137 Exam 2 Review Fibonacci Sequence and Chapters 6-10 NAMES: Show your work. Be sure to include appropriate units. 1. (3) My faucet runs at a rate of 5 gallons a minute. How many gallons a second
Math 137 Exam 2 Review Fibonacci Sequence and Chapters 6-10 NAMES: Show your work. Be sure to include appropriate units. 1. (3) My faucet runs at a rate of 5 gallons a minute. How many gallons a second
Nissan to make future New York taxis
 www.breaking News English.com Ready-to-use ESL/EFL Lessons by Sean Banville 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS The Breaking News English.com Resource Book http://www.breakingnewsenglish.com/book.html
www.breaking News English.com Ready-to-use ESL/EFL Lessons by Sean Banville 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS The Breaking News English.com Resource Book http://www.breakingnewsenglish.com/book.html
Diagnostic. Enlightenment. The Path to
 The Path to Diagnostic Enlightenment BY JORGE MENCHU If you don t know where you re going, any road will take you there. When it comes to automotive troubleshooting, the right road is the shortest path
The Path to Diagnostic Enlightenment BY JORGE MENCHU If you don t know where you re going, any road will take you there. When it comes to automotive troubleshooting, the right road is the shortest path
Teacher s Guide: Safest Generation Ad Activity
 Teacher s Guide: Safest Generation Ad Activity Introduction Today s 11- and 12-year-old preteens are very smart about vehicle safety. They have grown up using car seats and booster seats more consistently
Teacher s Guide: Safest Generation Ad Activity Introduction Today s 11- and 12-year-old preteens are very smart about vehicle safety. They have grown up using car seats and booster seats more consistently
